Short Introduction to Biostatistics

Biostatistical introduction includes Population Sample parametric non parametric +PV -PV sensitivity specificity and variable and research types.
Biostatistics an Introduction
1 Populations and Samples
A population is the set of all measurements that are of interest to a researcher. Normally the population is not observed, but we would like to make statements or conclusions/Inferences about it. Populations can be viewed as existing or conceptual. Existing populations are well-defined data sets that contain elements that could be explicitly identified.
Conceptual populations are sets of measures that do not exist but are visualized or imaginable. For example, this could be seen as a characteristic of all people with a disease, now or in the near future. It could also be seen as a result when a large group of subjects were treated. In this last scenario we are not giving treatment to all the issues, but we are interested in the results if it had been given to all of them.
Samples are infect observed sets of measurements/Calculations that are subsets of a corresponding population. Samples are used to describe and make inferences about the populations they come from. Statistical methods are based on these random samples drawn from the population.
Types of Variables
Quantitative Variables vs. Qualitative
The measurements to be made are called variables. This is related to the fact that we recognize that outcomes (often called endpoints in the medical world) vary by population. Variables can be classified as quantitative (numerical) or qualitative (categorical). The types of analyzes used depend on the type of variable being studied.
Furthermore, numerical variables can be divided into two types: continuous and discrete. Continuous variables are values that can be anywhere, corresponding to points on a line segment.Examples includes weight and diastolic/systolic blood pressure. Discrete variables are variables that can only take a finite (or countably infinite) number of outcomes.
Similarly, categorical variables are also commonly described in one of two ways: nominal and ordinal. Nominal variables have different levels that have no inherent order. Hair color and gender are examples of variables that would be called nominal. On the other hand, ordinal variables have levels that follow a specific order. Examples in the medical field generally relate to the degree of change in patients after treatment (such as: marked improvement, moderate improvement, no change, moderate deterioration, marked deterioration/death).
Dependent variables vs. independent
The variable(s) we measure as the outcome of interest is the dependent or response variable. The variable that determines the population that makes up a measure is the independent (or predictor) variable.
Parameters and Statistics
The parameters are descriptive numerical measures that correspond to populations. For numeric variables, there are two commonly reported types of descriptive measures: location and distribution. Site measurements describe the level of the "typical" measurement. Two widely studied measures are the mean (μ) and the median. The mean represents the arithmetic mean of all measurements in the population. The median represents the point at which half of the measurements are above and half of the measurements are below.
Two measures of the spread or spread of measurements in a population are the variance σ2 and the range. The variance measures the mean square distance of the measurements from the mean.Variance is the standard deviation (σ). While the range is the difference between the largest and the smallest measured value. A measure often referred to in research is the coefficient of variation. This measure is the ratio of the standard deviation to the mean, expressed as a percentage (CV = (σ /μ)100%). In general, small CV values are considered better.
Statistics infect are descriptive measures/calculations of numbers for samples. We will use the general notation θ ̂ to represent statistics.
For numerical measures, suppose we have n measures in our sample and denote them by y1, y2, . . . , and n. We then calculate the sample mean, variance, standard deviation, and coefficient of variation as follows:
For categorical variables with two levels, usually denoted as the presence and absence of the trait, we calculate the sample proportion of cases where the trait is present as (where x is the number in which the trait is present):
Graphic Techniques
Pie charts and histograms (or vertical bar charts) are often used for categorical variables to show the proportions of measurements that fall into specific categories (or levels of the variable). For numerical variables, pie charts and histograms can be used, where the measurements are “binned” into level ranges.
Basic Probability
Probability is used to measure the "likelihood" or "chances" of certain events (predetermined outcomes) of an experiment. The intersection of events A and B is the event where both A and B occur, where the notation is AB (sometimes written A ∩ B). The union of the events A and B is the event in which either A or B occurs, where the notation is A∪B. The complement of the event A is the event where A does not occur, where the notation is A. Some useful rules for obtaining these and other probabilities include:
• P(A∪B) = P(A) + P(B) − P(AB)
• P(A|B) = P(A occurs when B has occurred) = (P(AB))/(P(B)) (assuming that P(B) > 0)
• P(AB) = P(A)P(B|A) = P(B)P(A|B)
• P(A ̅) = 1 − P(A)
A specific situation occurs when events A and B are said to be independent. This is the case when P(A|B) = P(A) or equivalently P(B|A) = P(B), in this situation P(AB) = P(A)P(B).
Diagnostic tests
Diagnostic tests provide another situation in which the basic rules of probability can be applied. Subjects in a study group are determined to be sick (D+) or not sick (D−) according to a gold standard (a method that can reliably detect disease). The same subjects then undergo the newer (usually less traumatic) diagnostic test and are determined to be positive (T+) or negative (T-) for the disease. Patients are classified into one of four combinations of gold standard and diagnostic test results (D+T+, D+T−, D−T+, D−T−). There are more frequent formulas for probabilities are given below.
Sensitivity This is the probability that a person with the disease (D+) will give a true positive result based on the diagnostic test (T+). It is called Sensitivity = P(T+|D+).
Specificity This is the probability that a person without disease (D−) will give a true negative on the diagnostic test (T−). It is called specificity = P(T−|D−).
Positive predictive value This is the probability that a person who tests positive (T+) on a diagnostic test actually has the disease (D+). It is denoted as PV + = P(D+|T+).
Negative predictive value This is the probability that a person who tests negative for a diagnostic test (T-) does not actually have the disease (D-). It is denoted by PV − = P(D−|T−).
Overall Precision This is the probability that the test correctly diagnoses a randomly selected subject. It can be written as Precision = P(D+)Sensitivity + P(D−)Specificity.
Two commonly used terms related to diagnostic tests are false positive and false negative. T−). These are Positive and negative probabilities of these events can be written in terms of sensitivity and specificity:
P(false positive) = P(T+|D−) = 1−specificity
P(false negative) = P(T−|D+) = 1−sensitivity
If the study population is representative of the total population (in terms of the proportions with and without disease (P(D+) and P(D−))), the positive and negative values can be taken directly from the results table (see Example 1.8 However, in some situations, the two group sizes are chosen to be equal (equal numbers of diseased and non-diseased subjects.) In this case, we need to apply Bayes' rule to obtain the positive and negative predictive values. Assume that the proportion of diseased subjects in the actual population is known or well approximated and P(D+) is Then the positive and negative predictive values can be calculated as follows:
Basic study designs
Studies can generally be classified in two ways: observational or experimental. Observational studies are those in which researchers observe subjects and rank them based on the level of one (or more) explanatory variable(s) and a response of interest. Experimental studies can be viewed as studies in which an investigation is conducted an intervention (e.g., administering a specific drug treatment to a patient).
Observational Studies
In observational studies, the researcher identifies themes as they occur in nature and observes an interesting response for each theme. These types of studies can be prospective (first identifying the subject's level of explanation, then observing the outcome or response of interest) or retrospective (first observing the subject's outcomes, then gathering information on explanatory variables).
1. Case-control studies are generally retrospective and involve identifying subjects based on the magnitude of their response variable and measuring the magnitude of their explanatory variable (often thought of as a type of exposure). Typically, patients with a disease of interest (cases) are identified, as well as a similar group of patients in the same clinical setting who do not have the disease of interest (controls). Then all subjects are asked about their status considering a risk factor of interest. Example: Occurrence of cancer in smokers and non-smokers
2. Cohort studies are generally prospective and involve identifying subjects based on the level of their explanatory variables and obtaining the corresponding response outcome. These studies generally involve following subjects over a period of time to determine their outcome. For example, many studies have been conducted to compare breast cancer rates in women with breast implants and women without breast implants (Bryant and Brasher, 1995). Women with or without breast implants (explanatory variable) were identified and followed over time to determine whether or not they were diagnosed with breast cancer (response). Cohort studies are common when it is unethical to assign a disease (such as smoking or breast implants) to subjects, but it is possible to identify existing populations of such subjects. Cohort studies must have large sample sizes when the outcome of interest is rare in the population.
3. Cross-sectional studies involve randomly selecting subjects from a population and determining the levels of their explanatory and response variables. They are usually conducted retrospectively based on large medical databases at the health organization, state, or federal level. In these situations, they have a large number of people with extensive medical backgrounds on each topic. Topics are grouped and associations between variables are examined. Example: link between breast cancer and abortion.
Experimental studies
1. Experimental studies are those in which researchers perform an intervention on their subjects. Randomized clinical trials (RCTs) are controlled trials in which subjects are selected from a population of patients who meet some physical criteria and are randomly assigned to treatment groups. That is, the level of its explanatory variables is randomly assigned. These studies became popular in the late 1940s and are considered the gold standard of experimentation to determine cause and effect.
2. Parallel group studies, each subject receives a single treatment. Thus, the samples are independent (made up of different subjects) from one treatment to another.
3. In crossover studies, each subject receives each treatment and acts as their control. In these studies, the samples are considered paired or blocked (composed of the same subjects).
4. Historical control studies involve the use of subjects who have been treated previously (or not) and whose information is used to compare a currently tested treatment. These types of studies can be classified in two ways: 1) with historical controls treated by the same physicians at the same center as the current trial patients, and 2) with historical controls treated by different investigators at other centers (Berry, 1990). . 'Literature controls', comparison groups derived from the medical literature, would fall into the second group.
Other study designs
The ethical issues of assigning patients inferior treatment led researchers to develop sequential designs that would allow them to end the study early if a clear treatment effect was observed, without losing the "statistical purity" of the experiment. In these studies, if a certain level of success of one treatment over the other is observed, the study ends and all patients receive the superior treatment.
Reliability and Validity
Validity and reliability are important in determining whether we are measuring the right thing, how consistent our measurements are, and whether we are observing a causal relationship between variables. Reliability refers to the degree to which the results of a test can be reproduced if the test were repeated on the same person under the same conditions. Validity is the extent to which a concept, conclusion, or measure is well-supported and likely to accurately represent the real world. Internal validity refers to the extent to which we can conclude that changes in the independent variable(s) cause changes in the response variable.Read More


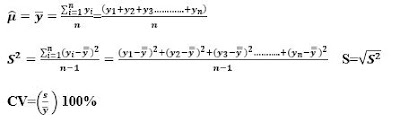




Give your opinion if have any.